賭王為什么能贏？
上書房咨詢 2020-06-01 17:22:48
北京時間5月26日，港澳知名愛國企業家、第9屆至第11屆全國政協常委何鴻燊在香港養和醫院逝世，享年98歲。何鴻燊去世的消息傳出后，港股博彩股出現異動，港股中華博彩指數盤中拉升，漲幅超過4%。賭王旗下的澳博控股漲幅一度飆高至超過8%，和何鴻燊家族相關的公司股價也出現大漲，其中信德集團漲幅擴大至超過20%，該公司重要股東之一為何鴻燊之女何超瓊。
說到博彩業，受到90年代香港電影的影響，很多人會有這樣的刻板印象：
所以，2020年了，還認為賭王賺錢就是在出老千嗎？
其實，現代賭場有由政府發布專門的牌照，已經不是過去處于灰色地帶時依靠老千、坐莊來盈利，賭場更多的是依靠數理基礎來和多種業態組合來實現盈利。
電影《賭神》、《賭圣》、《賭俠》劇照
博彩產業鏈
博彩業和旅游業兩種業態往往是互相依存，澳門的旅游產業鏈就是以博彩為核心拉動餐飲、購物、股票、地產、休閑娛樂等各種消費。目前，澳門已經呈現出“后博彩時代”的特征，雖然博彩業仍然是經濟支柱，但是正在逐步向會展、休閑、旅游等綜合項目發展。
博彩業中賭馬的產業鏈是最長的，上游包括了繁育、飼養、訓練、馬匹交易，中游包括了賽事運營、賽事傳播、產地租賃、俱樂部等，下游產業鏈包括了博彩競技、娛樂觀光、文化周邊等。香港賽馬會成立130多年來，既滿足了市民的博彩需求，又配合港府打擊非法賭博，將市民博彩的金錢引入正途。目前，香港賽馬會成為香港特區單一納稅最多的機構。
隨著數字經濟的發展，博彩業與科技產業結合產生了新的商業模式和機會。比如中國福利彩票發行管理中心推出的視頻彩票（VLT）項目，充分利用電信行業的通訊系統，實現中心機房和各地視頻彩票銷售廳終端的實時鏈接，利用網絡為平臺并隨機產生中獎者。
莊家為什么能贏？
賭徒思維中的前后因果謬論
有一類電視節目是預測彩票號碼的規律，電視上的“專家”會煞有介事的列出以往幾期出現的彩票號碼，并據此推測已經出現數字在下一期不會出現。這是一種典型的前后因果謬論。事實上，兩次搖號的行為是獨立事件，下一次號碼出現的概率與上一次并沒有任何關系。也就是兩次出現的彩票號碼都是隨機的，上一次出現號碼其實并不會影響下一次號碼。
賭場經營基礎之大數法則
在隨機事件的大量重復出現中，往往呈現幾乎必然的規律，這個規律就是大數定律。大數定律是指在試驗不變的條件下，重復試驗多次，隨機事件的頻率近似于它的概率。這是伯努利在1713年提出的歷史上第一個極限定理，其數學含義是：當n足夠大的時候，事件A出現的頻率將幾乎接近于其發生的概率，既頻率的穩定性。
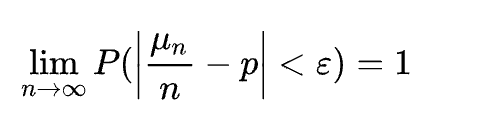
莊家不敗籌碼：凱利公式
在概率論中，凱利公式（也稱 “凱利方程式”）是一個在期望凈收益為正的獨立重復賭局中，使本金的長期增長率最大化的投注策略。該公式于 1956 年由約翰·拉里·凱利（John Larry Kelly）在《貝爾系統技術期刊》中發表，可以用來計算每次游戲中應投注的資金比例。設賭客的本金為N，投注比例為f，游戲每局有n種結果，第i種結果的凈收益率為ri，發生的概率為pi。則一局后對數本金 ln N 的增量（對數增長率）的數學期望為：
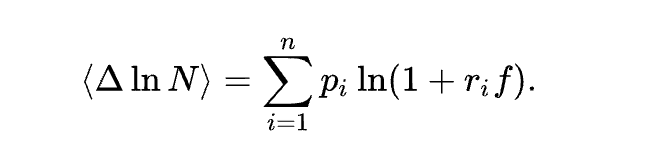
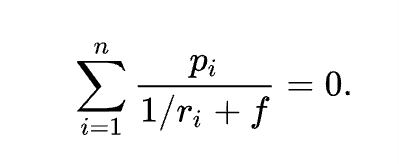
很多人說賭王運氣好，但他是這樣總結自己的：離不開多讀書、勤力、肯犧牲。
由于家庭背景優渥，何鴻燊從小過著衣食無憂的少爺生活，就讀于香港最好的學校——皇仁書院。小時候的何鴻燊不愛學習，當時成績很差，后家道沒落，何鴻燊嘗盡了世態炎涼，發奮讀書，以優秀的成績考入香港大學，并獲得獎學金。
由于抗戰爆發，香港失守，何鴻燊于1941年香港大學理科學院肄業后，來到澳門，進入澳門聯昌貿易公司工作。因一口流利的英語，他在公司擔任了秘書職務。何鴻燊的記憶力非常出眾，當時澳門的兩千多個電話號碼他能倒背如流，再加上善于交際，周旋四方，他很快成了這家公司的得力干將，并為公司立下汗馬功勞。
1961年，澳葡政府規定博彩業須通過專營制度實施，何鴻燊看準時機，重返澳門，與霍英東等人合作，一舉拿下賭場獨家專營權，邁出“賭王”之路的第一步。20世紀90年代初，又在澳門建立“皇宮賭場”等多個賭場。除香港和澳門外，何鴻燊亦在多個國家投資，包括越南、朝鮮、菲律賓、葡萄牙等。除博彩業之外，何鴻燊的產業還涉及房地產、建筑、船務、投資等多個領域。至2011年，其旗下的企業包括：澳門博彩控股有限公司、香港新濠國際集團、香港信德集團有限公司、澳門國際機場專營公司、王牌國際、澳門誠興銀行等。
在經營理念上，何鴻燊堅持保護并推廣澳門獨有的中西文化，因為他相信這是澳門持續發展的優勢所在，因此，他參與支持澳門各項旅游、文化、體育活動，其中包括贊助每年一度的澳門格蘭披治大賽車、澳門藝術節、澳門音樂節等。
荀子曰：君子博學深謀，修身端行，以俟其時。說的就是君子要多讀書、增長知識，端正品行、提高道德修養，以便等到機遇到來的時刻。賭王何鴻燊取得這樣的成績、成為澳門街的傳奇，就像賭王自己總結的“離不開多讀書、勤力、肯犧牲。”
作者：趙璐，經濟學博士，上書房信息咨詢公司合伙人，高級顧問
（本文部分圖文來源于網絡，如有侵權，請與我們聯系及時處理）
